ມຸມວົງໃນ Gears ແມ່ນຫຍັງ?

ໃນວິສະວະກຳເກຍ,ສະໜາມວົງມົນແມ່ນໜຶ່ງໃນການວັດແທກພື້ນຖານທີ່ສຸດທີ່ໃຊ້ເພື່ອອະທິບາຍໄລຍະຫ່າງຂອງແຂ້ວອ້ອມຮອບເກຍ. ມັນມີຜົນກະທົບໂດຍກົງຕໍ່ວິທີທີ່ເກຍປະສົມກັນ, ສົ່ງຕໍ່ການເຄື່ອນໄຫວ, ແລະຮັກສາການປະສານກັນໃນລະບົບສົ່ງກຳລັງ. ການເຂົ້າໃຈກ່ຽວກັບຄວາມສູງວົງມົນແມ່ນສິ່ງຈຳເປັນສຳລັບການອອກແບບເກຍທີ່ຊັດເຈນ ແລະ ຄວາມເຂົ້າກັນໄດ້ລະຫວ່າງເກຍທີ່ຈັບຄູ່ກັນ.

ຄໍານິຍາມຂອງວົງມົນ Pitch

ໄລຍະຫ່າງວົງມົນ (p) ຖືກນິຍາມວ່າເປັນໄລຍະຫ່າງລະຫວ່າງຈຸດໜຶ່ງເທິງແຂ້ວເກຍໜຶ່ງ ແລະ ຈຸດທີ່ສອດຄ້ອງກັນເທິງແຂ້ວຕໍ່ໄປ, ວັດແທກຕາມວົງມົນຂອງໄລຍະຫ່າງ.
ເທວົງມົນຕົວມັນເອງແມ່ນວົງມົນອ້າງອີງຈິນຕະນາການທີ່ສະແດງເຖິງຈຸດຕິດຕໍ່ລະຫວ່າງສອງເກຍທີ່ຈັບຄູ່ກັນ.

ເພື່ອໃຫ້ເກຍສອງອັນສາມາດປະສົມກັນໄດ້ຢ່າງຖືກຕ້ອງ, ໄລຍະຫ່າງວົງມົນຂອງພວກມັນຕ້ອງເທົ່າກັນເພື່ອຮັບປະກັນວ່າແຂ້ວແຕ່ລະອັນໃນເກຍໜຶ່ງພໍດີກັບຊ່ອງຫວ່າງລະຫວ່າງແຂ້ວຂອງອີກອັນໜຶ່ງຢ່າງສົມບູນ.

ສູດ ແລະ ການຄິດໄລ່

ສູດສຳລັບຄິດໄລ່ຄ່າ pitch ວົງມົນແມ່ນມາຈາກເສັ້ນຮອບວົງມົນຂອງ pitch ແລະ ຈຳນວນແຂ້ວ: p=πd​/N

ຢູ່ໃສ:

•  p = ຈັງຫວະວົງມົນ

• d = ເສັ້ນຜ່າສູນກາງຂອງສະໜາມ (ເສັ້ນຜ່າສູນກາງຂອງວົງມົນສະໜາມ)

• N = ຈຳນວນແຂ້ວ

ສູດນີ້ສະແດງໃຫ້ເຫັນວ່າໄລຍະຫ່າງຂອງວົງມົນແມ່ນຂຶ້ນກັບທັງຂະໜາດຂອງເກຍ ແລະ ຈຳນວນແຂ້ວທີ່ມັນມີ - ເກຍຂະໜາດໃຫຍ່ກວ່າ ຫຼື ແຂ້ວໜ້ອຍກວ່າຈະເຮັດໃຫ້ໄລຍະຫ່າງຂອງມຸມເກຍໃຫຍ່ກວ່າ.

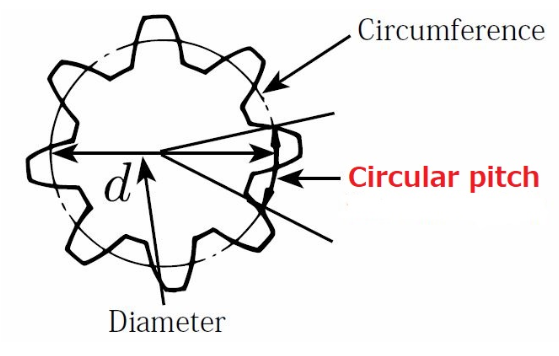
ຄວາມສຳພັນລະຫວ່າງມຸມວົງມົນ ແລະ ມຸມກົມ

ຄວາມສູງວົງມົນແມ່ນກ່ຽວຂ້ອງຢ່າງໃກ້ຊິດກັບການວັດແທກເກຍທົ່ວໄປອີກອັນໜຶ່ງທີ່ຮູ້ຈັກກັນໃນນາມ diametral pitch (P), ເຊິ່ງຖືກນໍາໃຊ້ຢ່າງກວ້າງຂວາງໃນລະບົບ imperial.

ໄລຍະຫ່າງລະຫວ່າງແຂ້ວ ແລະ ເສັ້ນຜ່າສູນກາງຂອງໄລຍະຫ່າງລະຫວ່າງແຂ້ວ ແມ່ນຈຳນວນແຂ້ວຕໍ່ນິ້ວຂອງເສັ້ນຜ່າສູນກາງຂອງໄລຍະຫ່າງລະຫວ່າງແຂ້ວ, ແລະ ທັງສອງແມ່ນເຊື່ອມຕໍ່ກັນທາງຄະນິດສາດດັ່ງຕໍ່ໄປນີ້: p=π/p

ຄວາມສຳພັນນີ້ຊ່ວຍໃຫ້ວິສະວະກອນສາມາດປ່ຽນລະຫວ່າງລະບົບເກຍທີ່ອີງໃສ່ແມັດຕຣິກ (ມຸມວົງມົນ) ແລະ ລະບົບເກຍທີ່ອີງໃສ່ອິມພີລຽວ (ມຸມເສັ້ນຜ່າສູນກາງ) ໄດ້ຢ່າງງ່າຍດາຍ.

ເວລາທີ່ຈະໃຊ້ Circular Pitch

ໃນຂະນະທີ່ລະດັບຄວາມສູງຂອງເສັ້ນຜ່າສູນກາງແມ່ນມາດຕະຖານໃນການນຳໃຊ້ເກຍທົ່ວໄປຫຼາຍຢ່າງ, ລະດັບຄວາມສູງຂອງວົງມົນສະເໜີຂໍ້ໄດ້ປຽບໃນກໍລະນີສະເພາະ:

1. ລະບົບການເຄື່ອນໄຫວແບບເສັ້ນຊື່ (Rack and Pinion):
ມຸມວົງມົນແມ່ນເໝາະສົມທີ່ສຸດສຳລັບລະບົບແຣັກ ແລະ ພີນຽນ, ບ່ອນທີ່ການເຄື່ອນທີ່ໝູນວຽນຖືກປ່ຽນເປັນການເຄື່ອນທີ່ເສັ້ນຊື່. ການໃຊ້ມຸມວົງມົນເຮັດໃຫ້ການຈັດດັດຊະນີ ແລະ ຕຳແໜ່ງງ່າຍຂຶ້ນ, ຍ້ອນວ່າແຕ່ລະການໝູນສອດຄ່ອງກັບໄລຍະທາງເສັ້ນຊື່ຄົງທີ່.
2. ເກຍຂະໜາດໃຫຍ່:
ສຳລັບເກຍຂະໜາດໃຫຍ່, ໄລຍະຫ່າງຂອງແຂ້ວວົງມົນໃຫ້ການວັດແທກໄລຍະຫ່າງຂອງແຂ້ວໂດຍກົງ, ເຮັດໃຫ້ມັນງ່າຍຕໍ່ການເຂົ້າໃຈ ແລະ ຕີຄວາມໝາຍໄດ້ຫຼາຍກ່ວາໄລຍະຫ່າງຂອງແຂ້ວເສັ້ນຜ່າສູນກາງ.
3. ການອອກແບບທີ່ອີງໃສ່ແມັດຕຣິກ:
ໃນລະບົບວິສະວະກຳແມັດຕຣິກ, ຄວາມສູງວົງມົນແມ່ນຫົວໜ່ວຍວັດແທກທີ່ຕ້ອງການ, ເຊິ່ງໃຫ້ຄວາມສອດຄ່ອງໃນຂະໜາດເກຍ ແລະ ການຄິດໄລ່.

ໄລຍະຫ່າງວົງມົນເປັນຕົວກໍານົດທີ່ສໍາຄັນໃນຮູບຮ່າງຂອງເກຍ, ເຊິ່ງກໍານົດວ່າແຂ້ວມີໄລຍະຫ່າງແນວໃດ ແລະ ເກຍສອງອັນມີຄວາມລຽບງ່າຍແນວໃດ. ການຄວບຄຸມການວັດແທກທີ່ຊັດເຈນນີ້ຮັບປະກັນການໂອນຍ້າຍການເຄື່ອນໄຫວທີ່ມີປະສິດທິພາບ, ການສວມໃສ່ໜ້ອຍທີ່ສຸດ, ແລະ ປະສິດທິພາບທີ່ໜ້າເຊື່ອຖືໃນທົ່ວລະບົບກົນຈັກ.

ທີ່ Belon Gear, ພວກເຮົາມີຄວາມຊ່ຽວຊານໃນການຜະລິດເກຍທີ່ມີຄວາມແມ່ນຍໍາສູງດ້ວຍຮູບຮ່າງແຂ້ວທີ່ດີທີ່ສຸດ—ຮັບປະກັນຄວາມສະໝໍ່າສະເໝີຂອງວົງມົນ ແລະ ປະສິດທິພາບຂອງຕາໜ່າງທີ່ບໍ່ມີຂໍ້ບົກຜ່ອງສຳລັບການນຳໃຊ້ໃນລົດຍົນ, ຫຸ່ນຍົນ, ແລະ ເຄື່ອງຈັກອຸດສາຫະກຳ.